Theorem 1.1.4: De Morgan's Laws
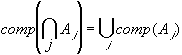 i.e. the complement of the intersection
of any number of sets equals the union of their complements.
i.e. the complement of the intersection
of any number of sets equals the union of their complements.
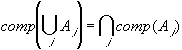 i.e. the complement of the union of any
number of sets equals the intersection of their complements.
i.e. the complement of the union of any
number of sets equals the intersection of their complements.
Proof:
We will prove two set-inequalities to prove equality of the left and right hand sides.- Take x contained in the complement of the intersection of all sets Aj, i.e. x is not in the intersection of all Aj. Then there must be at least one set Aj that does not contain x (because if all Aj would contain x then x would be in their intersection as well). Call this set A. Since x is not in A, x is in the complement of A. But then x is also in the union of all complements of Aj, because A is one of those sets. This proves that the left hand set is contained in the righ one.
- Now take x contained in the union of all complements of Aj. That means there is at least one complement that contains x, or in other words, at least one of the Aj does not contain x. But then x is not in the intersection of all Aj, and hence it must be in the complement of that intersection. That proves the other inequality, and hence both sets must be equal.

 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of