Examples 1.2.7(a):
If the graph of a function is known, how can you decide whether a function is
one-to-one (injective) or onto (surjective) ?
Injection
If a horizontal line intersects the graph of a function in more than one place, then there are two different points a and b for which f(a) = f(b), but a # b. Then the function is not one-to-one.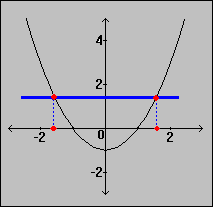 Not a one-to-one function
Not a one-to-one function
Surjection
If you place a light on the left and on the right hand side of the coordinate system, then the shadow of the graph on the y axis is the image of the domain of the function. If that shadow covers the range of the function, then the function is onto.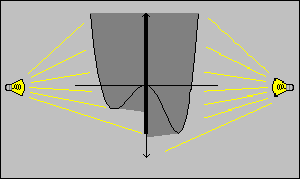 Not an onto function
(if range is R)
Not an onto function
(if range is R)
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of