Example 1.2.2: Multiplication in 2-D and C

Explore the differences between complex multiplication in C, the dot-product in R², and the cross-product in R² as embedded in R³.
Context

We now have four types of "multiplication" for vectors (x,y) in R².

Dot Product

For 'standard' R² vectors we have the (hopefully) familiar dot product:

(x,y) (u,v) = xu + yv

This type of multiplication results in a number (scalar), not a vector. It is therefore not useful for our purpose, since we need multiplication to result in another vector.

Geometrically the dot product gives the (cos of the) angle between (x,y) and (u,v). Useful indeed, but not for our current purpose.

Cross Product

If we think of 2-D vectors (x,y) as 3-D vectors with 0 as third component (x,y,0) we have the cross product:

(x,y,z) 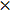(u,v,w) = (yw-zv, -xw+zu, xv-yu)

This type of product does yield a vector alright. But if we consider vectors whose third components are zero, such as (x,y,0) and (u,v,0) we get:

(x,y,0) 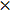(u,v,0) = (0-0, -0+0, xv-yu) = (0,0,xv-yu)

i.e. while the first two vectors live in the xy-plane, the result of a cross product lives perpendicular to that plane! Again, the result of our cross-product is not in our embedded R² (third component is not zero), so this product is no good (for our current purposes), too.

Silly Product

We already discussed the silly multiplication:

(x,y) (u,v) = (xu, yv)

which would violate the field axioms, so - definitely no good.

Complex Product

The original definition of complex multiplication

(x,y) (u,v) = (xu - yv, xv + yu)

will be the one that turns the usual 2-dimensional plane into the complex plane. We will discuss the geometric interpretation of this type of multiplication soon.

Interactive Complex Analysis, ver. 1.0.0
(c) 2006-2007, Bert G. Wachsmuth
Page last modified: May 29, 2007