Home -> Workshops -> Chaos and Fractals
Chaos and Fractals: Complex Dynamic Systems
Bert G. Wachsmuth
Department of Mathematics and Computer Science
Seton Hall University
Setup: Suppose
is a family of functions, and
. Study the orbits of
:
We will study the following two basic question:
 | fix the parameter c, what about the orbits of  for
various  's |
| fix a point  , what about the orbits of  for different values of c |
Example: Take the quadratic family
and
fix c = 0: 
.
Clearly f(0) = 0 and f(1) = 1, so the orbit of 0 is {0, 0, 0 …} and the orbit of 1 is {1, 1, 1 …}. Also, f(-1) = 1, so the orbit of -1 is {-1, 1, 1, 1 …}. Moreover, if
the orbit wil converge to 0, and if
the orbit will converge to positive infinity.
Definition: If 
is differentiable, and 
is a fixed point, i.e. 
, then:
| if  then  is called an
attracting fixed point |
| if  then  is called a
repelling fixed point |
| if  then  is called a
non-hyperbolic fixed point |
If 
is an attracting fixed point then the set of all
points whose orbit converges to is called the basin of
attraction of 
Example: Take the quadratic family
and
fix c = -2: 
.
We can easily find the fixed points and periodic points of higher order using Maple …
Example: Take 
. Then 
so that the period points of period n are
| infinitely many period points |
| period points are dense in  |
| and periodic points are repelling. |
Chaotic Dynamical Systems: 
is called
chaotic if:
| f has sensitive dependence on initial conditions |
| period points are dense in D |
| f is topologically transitive (technical) |
Example: 
is chaotic (call the function
f for short):
|
|
so that f also has a dense number of repelling periodic points in [-2, 2]
Question: How does the quadratic family 
go from completely simply (c = 0) to chaotic (c = -2) ? In other words, we now want to
look at the second question: fix 
and vary the parameter.
The best point to be fixed is the critical point where 
Bifurcation Diagram
Example: 
, fix critical point 
, vary c from 0 to -2:
Bifurcation Applet
|
Algorithm for Picture:
| Start with c = 0 |
| Compute sequence  without plotting |
| Compute sequence  and plot orbits |
| Replace c by c - (something) and repeat |
Sarkovskii's Theorem
Reorder the natural number as follows (Sarkovskii Ordering):
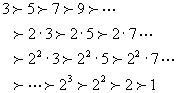
Then if
is continuous, and f has a period point of period k, then f also has periodic points of period l for all
in the Sarkovskii ordering.
Consequences:
If f has period 3, then f has periodic points of any period
If f has only finitely many periodic points, then these points are powers of 2
If f "wants" to have infinitely many periodic points, it must happen via "period-doubling" bifurcation
Iterations of Complex Functions
Same setup as before, but 
. Talking about families of
(analytic) function in C:
A family 
of analytic functions is normal:
is equicontinuous
omits more than 2 points (Montel's Theorem)
Example: 
with c = 0 and z in the complex plane. Inside
of unit circle and outside of unit circle is where the family is normal. Interior of unit
circle is the basin of attraction for fixed point z = 0, outside of unit circle is basin
of attraction for fixed point infinity.
In particular, equicontinuity implies that there is no sensitive dependence on initial conditions, therefore: normal families are not chaotic.
Definition:
| Fatou Set:  |
| Julia Set:  = complement of Fatou Set |
Originally by Fatou and Gaston Julia, 1920's.
Facts about the Fatou Set:
| Number of components of F is either infinite or less than or equal to 2 |
| F can be decomposed into attracting domains, superattracting domains, parabolic domains, Siegel disks, and Herman rings. The dynamics on each of these pieces of F is understood. |
Facts about the Julia Set:
|  where  (basin of
attraction) |
| J is the closure of all repelling periodic points |
| If the orbits of finite critical points are unbounded, then J is totally disconnected. If these orbits are bounded, J is connected |
| If  then  |
| J is the set where "chaos" takes place |
Algorithm to generate J:
| Choose a point  in C |
| Iterate  some 50 times, check if orbit is larger than,
say, 10 |
| If orbit is larger than 10, color  black. Otherwise color
 according to when it is larger than 10 |
| Choose another and continue |
The Mandelbrot Set
Consider the function 
. Then infinity is an attracting
fixed point, regardless of c, and 0 is the only critical point. Julia set is the boundary
of the basin of attraction of infinity, and it is either connected or totally
disconnected. For this particular family of functions, define:
Then the boundary of 
is the Julia set for this
particular c, and the set M in parameter space is called the Mandelbrot set.
Algorithm to generate M:
Fix
(the critical point). Choose a parameter
Iterate 50 times. If orbit is bounded, color
black. Otherwise, color
depending on when it's bigger than, say, 10.
Mandelbrot Applet:
|
It is interesting to put the Mandelbrot set and the Bifucation diagram right on top of eachother, using exactly the same scale. There you can see that the big cardiot region of the Mandelbrot set corresponds to Julia sets with one attracting fixed point, the second circular bulb corresponds to areas with an attracting orbit of period 2, and so on.
The Henon Map
Setup: The family of Henon Maps is defined as
Simple Facts:
| Almost affine map |
| Has an inverse map |
| WOLOG:  |
| If b = 0, then  is topologically conjugate to  |
| There is no "distinguished" point (such as the critical point). |
| When varying the parameters, we get: |
| If  then H has no fixed points |
| If  then H has one real fixed point |
| If  then H has two fixed points (a sink and a saddle) |
| If  then H has two fixed points (saddles) and a periodic
two orbit |
Simple Definitions:
Compute Eigenvalues
of the Jacobian matrix
Note that
If
is a fixed point, then:
| If  , the fixed point is attracting (and there is a basin
of attraction), or a sink |
| If  , the fixed point is repelling (and there is a basin
of attraction for the inverse function), or a source |
| If  , the fixed point is a saddle point (and there is a
stable and unstable manifold in the direction of the Eigenvectors corresponding to the
Eigenvalues) |
| If  or  , the fixed point
is non-hyperbolic (and difficult) |
Theorem:
There is a combination of (a, b) near b = 0.3 and a = -1.4 where the map is chaotic and the iterates has a "strange attractor".
A strange attractor is a set that attracts an open neighborhood, but is not the union of sinks.
Hanon Applet:
|
Bert G. Wachsmuth (bgw)
March 27, 1999