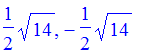
Exam 3 - Keys for Practice Exam

P. 543 - (Quadratic Equation)

1. Solve 2*x^2-7=0

> solve(2*x^2-7=0);

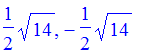
2. Solve 14*x^2 + 5*x = 0

> solve(14*x^2 + 5*x = 0);

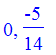
3. Solve x^2-12*x+36 = 9

> x^2 - 12*x + 36 = 9;
x^2 - 12*x + 36 - 9 = 0;
solve(x^2 - 12*x + 27 = 0);

9. Complete the square for x^2 - 12*x

> x^2 - 12*x:
x^2 - 12*x + 36 - 36:
factor(x^2-12*x+36) - 36;

23. Graph f(x) = -3 * (x+2)^2 + 4

> expand(-3*(x+2)^2+4);

The x-coord. of vertex is 12 / (-6) = -2. The y intercept is y=-8. To find x-intercept, we solve for zero:

> solve(-3*x^2-12*x-8=0);
evalf(%);

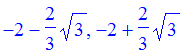
> plot(-3*x^2-12*x-8, x=-6..2);

>

24. Graph f(x) = 2*x^2 -12*x+23

The x-coord. of vertex is 12/4 = 3. The y-intercept is y = 23. To find the x-intercepts, we solve for zero:

> solve(2*x^2 -12*x+23 = 0);

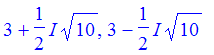
The solutions are imaginary numbers, so no intersections with x-axis. The final graph looks like:

> plot(2*x^2 -12*x+23,x=0..6);

25. Find x and y intercepts for f(x) = x^2 - 9*x + 14

The y-intercept is 14 (always easy). To find the x-intercepts, we solve for zero:

> solve(x^2 - 9*x + 14 = 0);

P. 544 - (Quadratic Equations and Inequalities)

1. Solve 3*x^2 - 16 = 0

> solve(3*x^2 - 16 = 0);

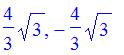
2. Solve 4*x*(x-2) - 3*x*(x+1) = -18

> expand(4*x*(x-2) - 3*x*(x+1) = -18);

> solve(x^2 - 11*x + 18 = 0);

3. Solve x^2 + x + 1 = 0

> solve(x^2+x+1=0);

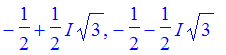
8. Complete the square for x^2 + 14*x

> x^2 + 14*x:
x^2 + 14*x + 49 - 49:
factor(x^2 + 14*x + 49) - 49;

16. Graph f(x) = 4*(x-2)^2 + 5

> expand(4*(x-2)^2 + 5);

> plot(4*x^2-16*x+21,x=0..4);

18. Find x-and y-intercept(s) of f(x) = x^2 - x - 6. The y-intercept is -6, for the x-intercept we solve

> solve(x^2 - x - 6 = 0);

23. Solve x^2 + 5*x <= 6

> solve(x^2 + 5*x <= 6);

24. Solve x - 1/x > 0

> x - 1/x = (x^2 - 1)/x;

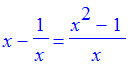
> solve((x^2 - 1)/x > 0);

P. 539 - (Solving Inequalities)

6. x^2 + x - 2 < 9 - first solve x^2 + x -11 = 0

> solve(x^2 + x - 2 < 9);

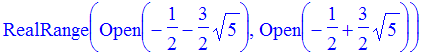
8. 4-x^2 >= 0 - special points are -2 and +2

> solve(4-x^2 >= 0);

10. x^2 + 6*x + 9 < 0 - has no solution

> solve(x^2 + 6*x + 9 < 0);

14. 5x(x+1)(x-1) > 0 - special points are 0, -1, and 1.

> solve(5*x*(x+1)*(x-1) > 0);

15. (x+3)(x-2)(x+1) > 0 - special points are -3, 2, and -1

> solve((x+3)*(x-2)*(x+1) > 0);

21. (x+1)/(x-5) >= 0 - special points are -1 and 5

> solve((x+1)/(x-5) >= 0);

27. (x-2) (x+1) / (x-5) <=0 - special points are 2, -1, and 5

> solve((x-2)*(x+1)/(x-5) <= 0);

28. (x+4)(x-1) / (x+3) >= 0 - special points are -4, 1, and -3

> solve((x+4)*(x-1)/(x+3) >= 0);

P. 528 - (Max/Min Programs)

1. If x is the number of months after January 2001, the a certain share price is V(x) = x^2 - 6*x + 13. What's the lowest value V will reach, and when will that occur? It's a parabola, opening up, so the minimum is at the vertex:

> x := 6/2;
V(x) := x^2 - 6*x + 13;

>

4. Profit is the difference between revenue R(x) and cost C(x). Given that R(x) = 1000*x - x^2 and C(x) = 3000 + 20*x, find the total profit, the maximum profit, and for which x it occurs.

> restart;
R(x) := 1000*x-x^2;
C(x) := 3000 + 20*x;
P(x) := R(x) - C(x);

This is a parabola opening down, with vertex at x = 490. The max. profit therefore is:

> P := x -> 980*x-x^2-3000;
P(490);

>

7. Farmer wants to enclose a retangular garden, one side being a barn. He has 40ft of fence. What's the max. area that can be enclosed?

> 2*x + y = 40;

> solve(%, y);

> A := (-2*x+40) * x;

> expand(A);

Once again, this is a parabola going down, so the max. is at the vertex, which is x = 10. Then y = 20 and the max. area is 200 square feet.

11. What is the max. product of two numbers that add to 18?

If x, y are those numbers, then we know that x + y = 18 (or y = 18 - x). We want to find the max. product, i.e. P = x * (18 - x), which is a parabola going down:

> P := x * (18 - x);

> expand(%);

Thus, the vertex is a maximum, and is x = 9, so that the other number is 9 as well.

P. 612 - (Log and Exp functions)

7. Graph f(x) = 3^x + 1. It's a standard exp. function, shifted up by one.

> plot(3^x+1, x=-4..2,-1..10);

>

9. Graph y = log_5(x). It's a standard logarithm function.

> plot(log[5](x),x=0..10);

>

40.Graph f(x) = e^x - 1. Standard exp. function, shifted down by 1. Domain is all numbers, range all numbers bigger than -1.

> plot(exp(x)-1, x = -4..2);

>

41. Graph g(x) = 0.6 * ln(x). It's a standard log. function. Domain is all positive numbers, range is all numbers:

> plot(0.6*ln(x),x=0..10);

>

43. Solve 3^x = 1/9. Since 1/9 = 3^(-2), we have 3^x = 3^(-2), so that x = -2

> evalf(solve(3^x = 1/9, x));

>

45. log_x(32) = 5. We need to raise this to the exp. function base x on both sides, which gives 32 = x^5. Hence x = 2.

> solve(log[x](32) = 5, x);

>

47. 3*ln(x) = -6. First we divide by 3: ln(x) = -2. We then apply the exponential function on both sides, getting x = e^(-2)

> solve(3*ln(x) = -6, x);

>

53. log_3(2*x - 5) = 1. We apply the exp. function base 3 on both sides, so 2*x - 5 = 3. But then x = 4.

> solve(log[3](2*x-5)=1);

54. log_4(x) + log_4(x-6) = 2.

We apply the rules of logs to combine into a single log: log_4(x * (x-6)) = 2. Then we apply the ep. function base 4 on both sides: x*(x-6) = 4^2 = 16. Now it's a simple quadratic equation: x^2 - 6*x - 16 = 0. Because the domain of logs is all positive numbers, the solution is only the positive one, i.e. x = 8.

> solve(x^2 - 6*x - 16 = 0);

55. log(x) + log(x-15) = 2. It's the natural log (base 10). We apply the rules of log: log(x * (x-15) ) = 2. Then we apply 10^(...) on both sides, so: x*(x-15) = 10^2 = 100. Thus (again, only the positive number works):

> solve(x*(x-15) = 100);

>

56. log_3(x-4) = 3 - log_x(x+4). First we move the logs to the same side: log_3(x-4) + log(x+4) = 3. Then we combine, using prop. of logs: log_3((x-4) * (x+4)) = 3. Finally, we appy 3^(...) on both sides: (x-4)*(x+4) = 27, or x^2 - 16 = 27. But then x^2 = 43, so that x = sqrt(43).

P. 614 - (Log and Exp functions)

28. Graph f(x) = e^x + 3 and state domain and range. It's the regular exp. function, shifted up by three. Domain is all numbers, range is all numbers bigger than 3:

> plot(exp(x) + 3, x=-4..2,-1..10);

>

29. Graph g(x) = ln(x - 4) and state domain and range. It's the regular log. function, shifted to the right by 4. Domain is all numbers bigger than 4, range is all numbers:

> plot(ln(x-4),x=0..14);

>

33 . Solve log(x) = 4 . This is the common log (base 10), so that x = 10^4 = 10,000

34 . Solve 5^(4-3*x) = 125. Since 125 = 5^3 we have 5^(4-3*x) = 5^3, so that 4 - 3*x = 3, or x = 1/3.

37. Solve log(x-3) + log(x + 1) = log(5). This is equivalent to log( (x-3) * (x+1)) = log(5). Applying the exp. function base 10 on both sides gives: (x-3)*(x+1)=5, which is a regular quadratic equation:

> (x-3)*(x+1)=5;

> expand(%);

> solve(%, x);

It can't be -2, because that's not in the domain of log(x+1), so the single solution is x = 4.