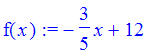
1. State, in your own words, the definition of the following terms:
a) slope of a line through two points (x, y) and (x, y)

If P1 = (x1, y1) and P2 = (x2, y2) then the slope m = (y2 - y1) / (x2 - x1)

b) function

A function is a rule that assigns to every number in its domain exactly one outcome number.

c) range and domain

Domain: All numbers for which a function is defined.

Range: All possible outcome numbers of a function.

d) linear function

A function with two variables, each raised to a power of at most 1.

e) monomial

Products of integer powers of variables and numbers

f) polynomial

Sums of monomials

2. Find the slope and y-intercept of the following lines, if possible, and graph them in the coordinate system provided:

2a)

f(x) := -3/5*x+12;

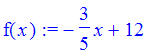
Has slope -3/5, y-intercept 12. The graph is:

> plot(-3/5*x+12, x=-3..3);

2. b)

> solve(-5*y - 2*x = 7, y);

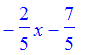
Slope is -2/5, y intercept -7/5. The graph is

> plot(-2/5*x - 7/5, x = -5..5);

2. c)

> solve(y + 5 = 7, y);

slope is zero, y intercept 2. The graph is:

> plot(2, x=-3..3);

2. d)

> solve(3 = x - 1,x);

Vertical line (undefined slope) through x = 4.

3. Find the linear equation describing the following lines
a) line with slope 4 containing (-2, -4)

y + 4 = 4 (x + 2)

3. b) line through (3, -1) and (4, -2)

> m := (-2 - (-1)) / (4 - 3);

> y +2 = m * (x - 4);

>

c) line containing (-3, 2) and parallel to the line 2x - 5y = 8

> solve(2*x - 5*y = 8, y);

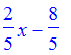
> m := 2/5;

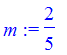
> y - 2 = m * (x + 3);

>

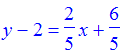
d) line containing (-3, 2) and perpendicular to the line 2x - 5y = 8

> m := -1 / (2/5);

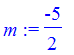
> y - 2 = m * (x + 3);

>

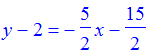
e) line through (1, 2) and perpendicular to the line through (-2, -2) and (3, 1)

> m := (1 - (-2)) / (3 - (-2));

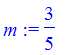
> m := -1 / (3/5);

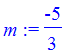
> y - 2 = m * (x - 1);

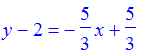
f) line through (-2, -2) and (3, -2)

m = 0, so it's a horizontal line passing through y = -2, so the equation is y = -2

g) line through (-2, -2) and (-2, 3)

m = 1/0 = undefined, so it's a vertical line passing through x = -2, so the equation is x = -2

4. For the following problems, evaluate the given function at the indicated position.

> f := x -> (x - 3) / (2*x - 5);

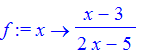
> f(0);

> f(3);

> f(-1);

> f(a+h);

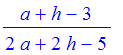
> g := t -> 5*t^2 + 4*t;

> g(0);

> g(-1);

> g(2*a);

> (g(a+h) - g(a-h)) / h;

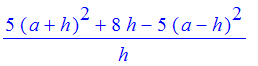
> simplify(%);

5. Which of the following graphs represent a functions, which ones not? For each graph representing a function, determine the range and domain of that function.

First is a function. Domain is all numbers, range is all numbers (it's hard to see, but that's what it seems like).

Second is not a function.

Third is a function, domain is -1 to 1, range is 0 to 1

Fourth is a function, domain is -1 to 2, range is the numbers {1, 2}

6. Solve the following systems of linear equations.

> solve( {2*x-3*y=0, -4*x+3*y=-1}, {x,y});

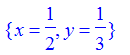
> solve( {2*x+y=6, 3*x+4*y=4}, {x, y});

> solve( {9*x-6*y=2, x=4*y+5}, {x,y});

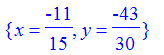
> solve( {0.2*x+0.3*y=1.7, 1/7*x+1/5*y=-29/35}, {x,y});

> solve( {3*y-2*x=6, 8*x-12*y=-24}, {x,y});

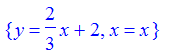
This means there are infinitely many solutions, or the lines are the same

> solve( {y=x+2, y-x=8}, {x,y});

This means there are no solutions, or the lines are parallel but not identical.

7. Solve the following inequalities and draw the solution set on a number line.

> solve(-4*y-3>=5, y);

> solve( -8*(2*x+3) + 6*(4-5*x) >= 2*(1-7*x)-4*(4+6*x), x);

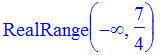
> solve(-15 < -4*x-5, x);solve(-4*x-5<1);

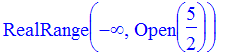
This means that the answer is (-3/2, 5/2).

> solve(-1/3 <= 1/6*x-1);solve(1/6*x-1<1/4);

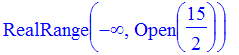
This means that the answer is (15/2, 4)

> solve(3*x-2 < 7);solve(x-2 > 4);

This means that the answer is (-infinity, 3) union (6, infinity)

> solve(abs(4*x-1) < 4.5);

> solve(abs(-5*t-3) > 10);

> solve(abs(2.1*x-7.9) < -2);

This means that there is no answer (obviously, since an absolute value is never negative)

>

8. Find the domains of the following functions:

> f(x) := (x-2)/(3-x);

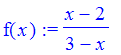
Domain is all numbers except 3.

> g(x) := sqrt(7-2*x);

> solve(7-2*x >= 0, x);

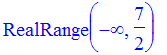
That's the domain (-infinity, 7/2].

> h(x) := sqrt(2*x-4) / (x-4);

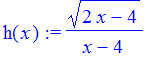
> solve(2*x-4 >= 0, x);

Thus, the domain is all numbers bigger than or equal to 2, except 4 (because of the denominator).

9. Perform the following operations

> expand((4*x-1) * (4*x+1));

> expand((a+b-1)*(a+b+1));

> expand((a^2+a-1)*(a^2+a*b+b^2));

> expand((x-2*y)*(x^2+1)*(3-2*y^2));

> factor(-2*x^3 + 4*x^2 - 2*x);

> factor(12*a^4-21*a^3-9*a^2);

> factor( 5*x^2*(x-6) + 10*x*(6-x));

> f := x -> x^2;

10. If a given function f has a graph as indicated, please graph the modified function

> plot({f(x), f(x)-2, f(x+1), f(x-2)+1, -f(x), f(-x)}, x=-4..4);

>