Limit Comparison Test
Suppose 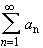 and
and
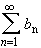 are two infinite series.
Suppose also that
are two infinite series.
Suppose also that
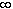 Then
Then
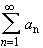 converges absolutely if and only if
converges absolutely if and only if
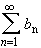 converges absolutely.
converges absolutely.
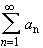 and
and
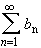 are two infinite series.
Suppose also that
are two infinite series.
Suppose also that
r = lim | a n / b n |exists and 0 < r <
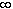 Then
Then
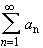 converges absolutely if and only if
converges absolutely if and only if
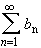 converges absolutely.
converges absolutely.
This test is more useful than the "direct" comparison test because you do not need to compare the terms of two series too carefully. It is sufficient if the two terms behave similar "in the long run".
| Examples 4.2.6: | |
| |
Since
r = lim | a n / b n |
exists, and r is between 0 and infinity there exist
constants c and C,
0 < c < C < 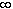 such that for some positive integer N we have:
such that for some positive integer N we have:
c < | a n / b n | < Cif n > N. Assume
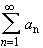 converges absolutely. From above we have that
converges absolutely. From above we have that
c | b n | < | an |for n > N. Hence,
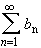 converges absolutely by the comparison test.
converges absolutely by the comparison test.
Assume
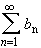 converges absolutely. From above we have that
converges absolutely. From above we have that
|a n | < C | b n |for n > N. But since the series C
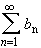 also converges absolutely, we can use again the comparison test to see
that
also converges absolutely, we can use again the comparison test to see
that
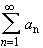 must converge absolutely.
must converge absolutely.
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of 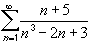 converge or diverge ?
converge or diverge ?
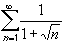 converge of diverge ?
converge of diverge ?
 p(n)
to converge or diverge ?
p(n)
to converge or diverge ?