Cauchy Condensation Test
Suppose
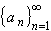 is a decreasing sequence of positive terms. Then the series
is a decreasing sequence of positive terms. Then the series
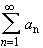 converges if and only if the series
converges if and only if the series
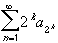 converges.
converges.
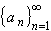 is a decreasing sequence of positive terms. Then the series
is a decreasing sequence of positive terms. Then the series
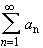 converges if and only if the series
converges if and only if the series
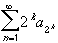 converges.
converges.
This test is rather specialized, just as Abel's Convergence Test. The main purpose of the Cauchy Condensation test is to prove that the p-series converges if p > 1.
| Example 4.2.8: | |
| |
Proof:
Assume that
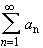 converges: We have
converges: We have
2k-1 a2k = a2k + a2k + a2k + ... + a2kbecause the sequence is decreasing. Hence, we have that
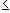
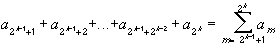
Now the partial sums on the right are bounded, by assumption. Hence the partial sums on the left are also bounded. Since all terms are positive, the partial sums now form an increasing sequence that is bounded above, hence it must converge. Multiplying the left sequence by 2 will not change convergence, and hence the series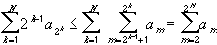
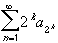 converges.
converges.
Assume that
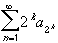 converges: We have
converges: We have
Therefore, similar to above, we get: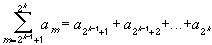
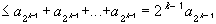
But now the sequence of partial sums on the right is bounded, by assumption. Therefore, the left side forms an increasing sequence that is bounded above, and therefore must converge.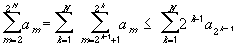
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of 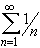 ,
list the terms
a4,
ak, and
a2k.
Then show that this series (called the harmonic series) diverges.
,
list the terms
a4,
ak, and
a2k.
Then show that this series (called the harmonic series) diverges.
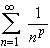 converge or diverge ? (In addition to the p-Series test , recall
the Geometric Series Test for this example)
converge or diverge ? (In addition to the p-Series test , recall
the Geometric Series Test for this example)