Examples 4.2.4(a):
Because | sin(x) | 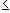 1
for all real number x, we have that
1
for all real number x, we have that
1 / 2 n sin(n) |But| 1 / 2 n |
.gif) is
a special case of the geometric series, which converges. Hence,
by the comparison test, the original series
is
a special case of the geometric series, which converges. Hence,
by the comparison test, the original series
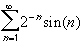 converges
absolutely.
converges
absolutely.
Note that, formally, we could say: Since
| 1 / 2 n sin(n) |for all n. We also have| 1 / 2 n |
|"Therefore", the series converges absolutely.|
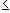
<
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of