Proposition 7.4.15: Measurable Functions are Almost Continuous
Suppose f is a measurable function defined on an interval
[a, b] such that the set where f is plus or minus
infinity has measure zero. Then, for any 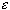 > 0
we can find a step function g and a continuous function h
such that
> 0
we can find a step function g and a continuous function h
such that
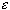 .
.
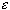 > 0
we can find a step function g and a continuous function h
such that
> 0
we can find a step function g and a continuous function h
such that
| f(x) - g(x) | <except on a set of measure less than
| f(x) - h(x) | <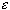
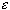 .
.
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of