Example 7.2.6(d): Applying Integration by Parts
As in the previous example, it seems that integration by parts does not apply because there is no product. But we can write sin5(x) = sin(x) sin4(x) and define the functionsThen G(x) = f(x) g(x) = -cos(x) sin4(x) and
- g'(x) = sin(x) so that g(x) = -cos(x)
- f(x) = sin4(x) so that f'(x) = 4 sin(x)3 cos(x)
It seems as if we are stuck. Not only did we get the original integralsin5(x) dx = -cos(x) sin4(x) + 4
sin(x)3 cos2(x) dx =
= -cos(x) sin4(x) + 4sin(x)3 (1 - sin2(x)) dx =
= -cos(x) sin4(x) + 4sin(x)3 dx - 4
sin5(x) dx
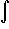 sin5(x) dx
back, but we introduced
sin5(x) dx
back, but we introduced
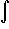 sin3(x) dx
which seems just about as complicated as the original integral. However, with a
little more abstraction we can solve the original problem "by magic".
sin3(x) dx
which seems just about as complicated as the original integral. However, with a
little more abstraction we can solve the original problem "by magic".
Let
Ik =Define the functionssink(x) dx =
sin(x) sink-1(x) dx
Then
- g'(x) = sin(x) so that g(x) = -cos(x)
- f(x) = sink-1(x) so that f'(x) = (k-1) cos(x) sink-2(x)
Ik = -cos(x) sink-1(x) + (k-1)Solving this expression for Ik we getcos2 sink-2(x) dx =
= -cos(x) sink-1(x) + (k-1)(1 - sin2) sink-2(x) dx =
= -cos(x) sink-1(x) + (k-1)sink-2(x) dx - (k-1)
sink(x) dx =
= -cos(x) sink-1(x) + (k-1) Ik-2 - (k-1) Ik
Ik = -1/k cos(x) sink-1(x) + (k-1)/k Ik-2But this is a recursive formula for computing Ik for any integer k. In particular we have
Indeed, a - cumbersome - check would show that
- I0 =
sin0(x) dx =
1 dx = x
- I1 =
sin1(x) dx = -cos(x)
- I2 = -1/2 cos(x) sin(x) + 1/2 I0 = -1/2 cos(x) sin(x) + 1/2 x
- I3 = -1/3 cos(x) sin2(x) + 2/3 I1 = -1/3 cos(x) sin2(x) - 2/3 cos(x)
- I4 = -1/4 cos(x) sin3(x) + 3/4 I2 =
= -1/4 cos(x) sin3 + 3/4 (-1/2 cos(x) sin(x) + 1/2 x)- I5 = -1/5 cos(x) sin4(x) + 4/5 I3 =
= -1/5 cos(x) sin4(x) + 4/5 (-1/3 cos(x) sin2(x) - 2/3 cos(x))
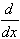 I5 = sin5,
so that our recursive formula and the resulting answer for our particular example seem
correct.
I5 = sin5,
so that our recursive formula and the resulting answer for our particular example seem
correct.
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of