Example 8.2.6 (a): Uniform Convergence and Sup Norm
Consider the sequence fn(x) = 1/n sin(n x):
- Show that the sequence converges uniformly to a differentiable limit function for all x.
- Show that the sequence of derivatives fn' does not converge to the derivative of the limit function.
This example is ready-made for our sup-norm because |sin(x)| < 1 for all x. As for our proof: the sequence converges uniformly to zero because:
||fn - f||D = ||1/n sin(n x) - 0||DThe sequence of derivatives is1/n
0
f '(x) = cos(n x)which does not converge (take for example x =
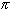 ).
).
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of