Example 8.4.7 (c): Using Taylor's Theorem
If the function
f(x) = 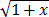 had a Taylor series
centered at c = 0, what would be its radius of convergence?
had a Taylor series
centered at c = 0, what would be its radius of convergence?
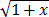 had a Taylor series
centered at c = 0, what would be its radius of convergence?
had a Taylor series
centered at c = 0, what would be its radius of convergence?
If the function had a Taylor series, the remainder would go to zero and
the function would be infinitely often differentiable. It is clear that
f(x) = 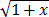 is (infinitely often)
differentiable for x > -1. Therefore the Taylor series centered at
c = 0 is not expected to converge at x = -1.
Therefore our guess for the radius of convergence is:
is (infinitely often)
differentiable for x > -1. Therefore the Taylor series centered at
c = 0 is not expected to converge at x = -1.
Therefore our guess for the radius of convergence is:
r = 1
For your enjoyment, the function does have a Taylor series and you can double-check that:
f(0) = 1,
f'(0) = 1/2,
for n > 1
Above you see how well the sixth-degree Taylor polynomial approximates the square-root function.
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of