Theorem 2.3.3: Induction Principle
Let S be a well-ordered set with the additional
property that every element except for the smallest one has an
immediate predecessor. Then: if Q is a property such
that:
- the smallest element of S has the property Q
- if s
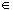 S
has property Q then the successor of s also has property
Q
S
has property Q then the successor of s also has property
Q
Proof:
It is not quite obvious what it is that we have to prove: we need to show that if a property holds for the smallest element of a well-ordered set S, and it holds for every successor of a general element of that set, then it is indeed true for the whole set S.We will prove this by contradiction: Suppose property Q is true for the smallest element of a well-ordered set S, denoted by the symbol 1. Suppose also that property Q is true for the successor n + 1 of the general element n of that set, if it is assumed to be true for that element n.
- Denote by E the set of all elements from S for which property Q is not true
For that element the property Q holds true, and therefore, being true for n - 1 it must be true for (n-1) + 1 = n, by assumption. Hence, the set E must be empty, and property Q is therefore true for all of S.
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of