Our proofs so far, for the most part, were mostly computational and did not require great ingenuity. But the proof of the second part of this statement is different, it needs some smart trickery. The first part, though, is straight foward. Let

w_n = cis(2/n)

Then

w_n^k = cis(2 k / n)

by DeMoivre's formula. Therefore, using that formula again:

(w_n^k)ⁿ = cis(2 k n / n) = cis(2 k ) = 1

for all positive integers k. Thus, each w_n^k is an n-th root of unity (because its n-th power is 1). And if k = 0, 1, 2, ..., n-1 then all w_n^k are distinct so that we have indeed found n different n-th roots of 1.

As for the second part, let

S_n = 1 + z + z² + z³ + ... + zⁿ

Then

z S_n = z + z² + z³ + ... + zⁿ + zⁿ⁺¹

Subtracting terms we get

S_n - z S_n = S_n(1-z) = 1 - zⁿ⁺¹

because all terms of S_n - z S_n except the first and last remain. But then, for z 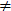1

S_n = 1 + z + z² + z³ + ... + zⁿ = ^1-zn+1/_1-z

or equivalently S_n-1 = ^1-zn/_1-z. But then

(1-z) S_n-1 = (1-z)(1 + z + z² + z³ + ... + z^n-1) = 1 - zⁿ

If we now substitute w_n = cis(2/n) for n > 0 we have

(1-w_n)(1 + w_n + w_n² + ... + w_n^n-1) = 1 - (w_n)ⁿ = 0

because w_nⁿ = 1. But now our statement follows because w_n 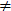1 if n > 0. Now that's a proof.

Here are, for example, the eight roots of z⁸=1:

The 8 roots of z8=1	Sum of 8-th roots is zero

Incidentally, the fact that

(1-z)(1 + z + z² + z³ + ... + z^n-1) = 1 - zⁿ

can also be confirmed by "long division" - but who wants to do that ...