For any positive integer n and any non-zero complex number a = r cis(t) the equation zn = a has exactly n distinct roots given by:z =where k = 0, 1, 2, ... n-1.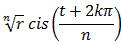
Proposition 1.2.16: Finding Roots |
For any positive integer n and any non-zero complex number a = r cis(t) the equation zn = a has exactly n distinct roots given by:z =where k = 0, 1, 2, ... n-1. |
As is often the case in mathematics, the proof is easy if you happen to know the correct answer by working backwords. In our case we start by saying: let a = r cis(t) and define
z =Then, according to our theorem on muliplying geometrically we have: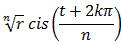
for all k = 0, 1, 2, ... n-1 because of the periodicity of cos.
It is more enlightning to try to understand how this theorem works geometrically. For simplicity take a = cis(t), i.e. |a|=1:
To find an n-th root of a vector with angle t, divide that angle by nThat gives you the first root.
Divide the unit circle into n equally spaced pieces, starting at the first angle t/n
That will be your n-roots total. As an example, let's find the three third-roots of i, i.e. we want to find all solutions to z3 = i.
Step 1: Draw the vector i
Step 2: Divide the angle by 3 for your first root
Step 3: Draw 3 equally spaced segments, starting at the first root