DeMoivre's Formula is quite something. It says that if you take a number on the unit circle (i.e. with lenght 1) with initial argument (angle) t and multiply it by itself, it simply rotates around the unit circle by that angle t. Each time you multiply the number by itself, the vector rotates another t degrees. In other words, in this case the power operator results in a simple rotation.

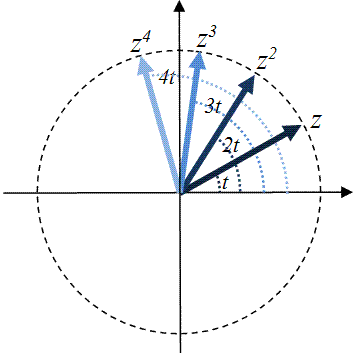
Powers of a vector z with |z|=1

The proof of the formula follows directly from our previous theorem on multiplying directly. We showed that if z = r cis(t) then zⁿ = rⁿ cis(nt). Now let r=1 and substitute the definition of cis to get DeMoivre's Formula.