Example 1.2.17 (b): Finding roots geometrically

Find all 4 fourth-roots of -1 and draw them geometrically.
Context Context

With -1 = 1 cis() the formula gives us four roots:


z1 = cis(/4)
z2 = cis(( + 2)/4) = cis(3/4)
z3 = cis(( + 4)/4) = cis(5/4)
z4 = cis(( + 6)/4) = cis(7/4)

Note that the next root in that pattern equals z1 since

cis(/4) = cis(9/4)

But let's to do this geometrically, as before. We have -1 = cis().

Step 1: Draw the vector -1


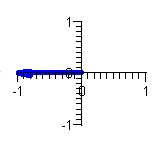
a = -1

Step 2: Divide the angle by 4 (lengh = 1)


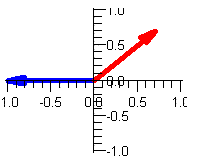
z1 = cis(/4)

Step 3: Draw 3 equally spaced segments, starting at the first root



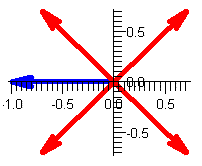
z1 = cis(/4)
z2 = cis(3/4)
z3 = cis(5/4)
z3 = cis(7/4)

Interactive Complex Analysis, ver. 1.0.0
(c) 2006-2007, Bert G. Wachsmuth
Page last modified: May 29, 2007