With 8 = 8 cis(0) the formula gives us three roots:

z₁ = 2 cis(0/3) = 2
z₂ = 2 cis((0 + 2)/3) = 2 cis(2/3)
z₃ = 2 cis((0 + 4)/3) = 2 cis(4/3)

But it's more fun to do this geometrically. We have 8 = 8 cis(0).

Step 1: Draw the vector 8

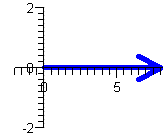
a = 8

Step 2: Divide the angle by 3 and adjust the lengh

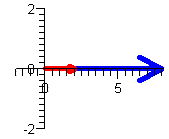
z₁ = 2

Step 3: Draw 3 equally spaced segments, starting at the first root

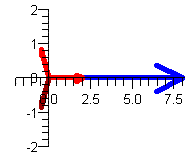
z₁ = 2
z₂ = 2 cis(2/3)
z₃ = 2 cis(4/3)

We already figured out the three third roots of i so we won't have to do that again.