Convert the following numbers into the indicated coordinates and draw them in the complex plane:
- z=(-2,0), w=(0,-2), v=(3,4), u=(3,-4) from rectangular to polar
Context
Example 1.2.11 (b): Polar coordinates examples |
Convert the following numbers into the indicated coordinates and draw them in the complex plane: |
Conversion from polar to rectangular is a 2-step process. If x=Re(z) is not zero, we compute
r =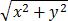
= arctan(|y|/|x|)
and then we adjust the angle depending on which quadrant our vector is in. If Re(z) = 0 we know the angle right away.
For z:
 |
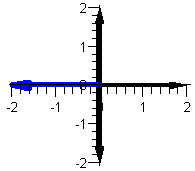We have that x=-2 and y=0 so that:
r =Since z is on the negative x-axis, it is in the second quadrant so the angle is t=  -0=.
Thus z=(2,) in polar coordinates.
|
 |
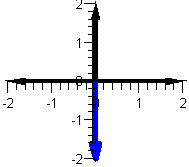We have that x=0 and y=-2 so that:
r =As for the angle we have that Re(w)=0 and Im(w)<0 so that the angle is t=- /2. Thus
w=(2,-/2) in polar coordinates.
|
 |
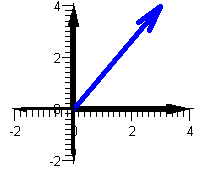We have that x=3 and y=4 so that:
r =This time v is in the first quadrant so the angle (in radiant) is t=0.93 (approx.). Thus w=(5,0.93) in polar coordinates. Note that an angle of t=0.93 is just a little less than /3.
|
For u:
 |
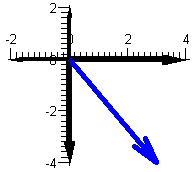We have that x=3 and y=-4 so that as before:
r =But this time u is in the fourth quadrant so the angle (in radiant) is t=-0.93 (approx). Thus w=(5,-0.93) in polar coordinates. Note that an angle of -t=0.93 is just about the same as - /3.
|
= 2
= 5
0.93 (radiant)