Conversion from polar to rectangular is easy, using

x = r cos(t)
y = r sin(t)

For z: we have that length r=2 and angle t=0 so that:

x = r cos(t) = 2 cos(0) = 2
y = r sin(t) = 2 sin(0) = 0

For w: we have that length r=3 and angle t= so that:

x = r cos(t) = 3 cos() = -3
y = r sin(t) = 3 sin() = 0

For v: we have that length r=2 and angle t=5/6 so that:

x = r cos(t) = 2 cos(5/6) = -2*1/2* = -
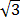
y = r sin(t) = 2 sin(5/6) = 2*1/2 = 1

For u: we have that length r=2 and angle t=-3/4 so that:

x = r cos(t) = 2 cos(-3/4) = 2*(-1/2)* = -
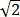
y = r sin(t) = 2 sin(-3/4) = 2*(-1/2)* = -

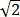
You should confirm these computations by drawing the various vectors.