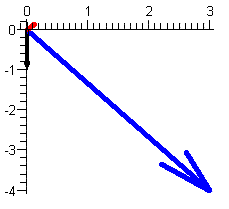
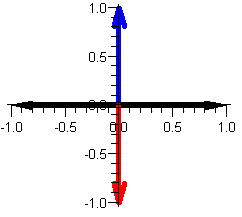
Let u = 3 - 4i and v = i, and w = -2. Draw 1/u, 1/v, 1/w and then describe how 1/z looks in relation to z for arbitrary complex numbers.
Example 1.2.4 (c): Complex numbers in the plane |
Let u = 3 - 4i and v = i, and w = -2. Draw 1/u, 1/v, 1/w and then describe how 1/z looks in relation to z for arbitrary complex numbers. |
 |
 |
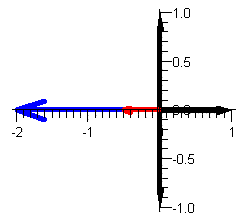 |
| u=3-4i (blue) and 1/u=1/5(3+4i) (red) | v=i (blue) and 1/v=-i (red) | w=-2 (blue) and 1/w=-1/2 |
 |
 |
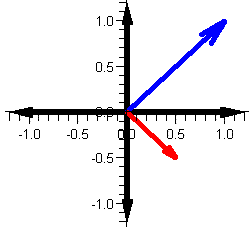
| 1+i (blue) and 1/(1+i) (red) | i-1 (blue) and 1/(i-1) (red) |