Example 1.2.14 (b): Multiplying geometrically

Draw the vectors zn, n=1, 2, ... 8 for z=cis(/4) and z=0.85 cis(/8)
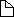Context Context

zn means to multiply z with itself, and we know how to interpret multiplication geometrically. Thus, with z=cis(/4) we have:

  • z=cis(/4)
  • z2=z*z= cis(/4)*cis(/4) = cis(/4+/4)= cis(/2)
  • z3=z*z2= cis(/4)*cis(/2) = cis(/4+/2)= cis(3/4)
  • z4=z*z3= cis(/4)*cis(3/4) = cis(/4+3/4)= cis()
  • z5=z*z4= cis(/4)*cis() = cis(/4+)= cis(5/4)
  • z6=z*z5= cis(/4)*cis(5/4) = cis(/4+5/4)= cis(3/2)
  • z7=z*z6= cis(/4)*cis(3/2) = cis(/4+3/2)= cis(7/4)
  • z8=z*z7= cis(/4)*cis(7/4) = cis(/4+7/4)= cis(2)=1

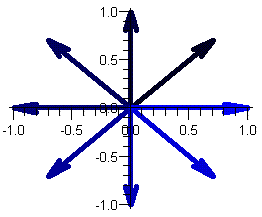The vector z=1/2 cis(/8) has similar powers, adjusting for the fact that its length is not one:

  • z=0.85 cis(/4)
  • z2=z*z= 0.85 cis(/4) * 0.85 cis(/4) = 0.852 cis(/4+/4)= 0.852 cis(/2)
  • z3=z*z2= 0.85 cis(/4) * 0.852 cis(/2) = 0.853 cis(/4+/2)= 0.853 cis(3/4)
  • z4=z*z3= 0.85 cis(/4) * 0.853 cis(3/4) = 0.854 cis(/4+3/4)= 0.854 cis()
  • z5=z*z4= 0.85 cis(/4) * 0.854 cis() = 0.855 cis(/4+)= 0.855 cis(5/4)
  • z6=z*z5= 0.85 cis(/4) * 0.855 cis(5/4) = 0.856 cis(/4+5/4)= 0.856 cis(3/2)
  • z7=z*z6= 0.85 cis(/4) * 0.856 cis(3/2) = 0.857 cis(/4+3/2)= 0.857 cis(7/4)
  • z8=z*z7= 0.85 cis(/4) * 0.857 cis(7/4) = 0.858 cis(/4+7/4)= 0.8580.852 cis(2)=1

Interactive Complex Analysis, ver. 1.0.0
(c) 2006-2007, Bert G. Wachsmuth
Page last modified: May 29, 2007