Example 1.2.8: Conjecture for multiplying geometrically |
Let z=1+i, w=1-i, and v=i. Compute and
visualize z*w, v*z, v*w,
z2, w2, and
v2. Try to come up with a conjecture how to visualize
multiplication of two general complex numbers.
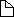Context
|
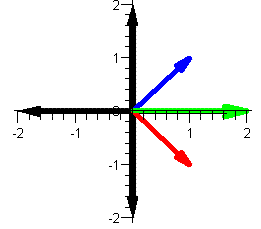
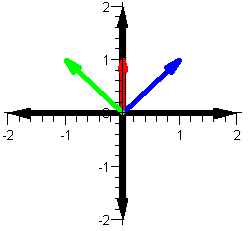
In the set of pictures below we multiply the red
and blue vectors together and display the
result as a green vector.
 |
 |
 |
| z (blue), w (red) and z*w (green) |
z (blue), v (red) and z*v (green) |
v (blue), w (red) and v*w (green) |
Now we square the blue vector (i.e. multiply it
with itself) and display the result as a green vector.
 |
 |
 |
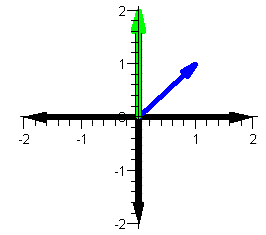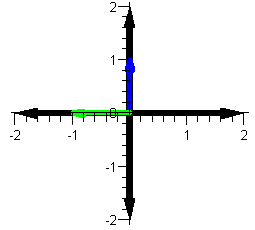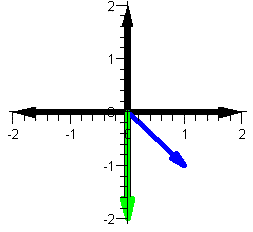| z (blue) and z2 (green) |
v (blue) and v2 (green) |
w (blue) and w2 (green) |
To come up with a conjecture is left to you. As a hint, ignore the lenghts
(at first) and focus on the angles the vectors make with the x-axis.
Once you think you got a handle on the angles, figure out the lenghts.
Interactive Complex Analysis, ver. 1.0.0
(c) 2006-2007, Bert G. Wachsmuth
Page last modified: May 29, 2007