8.4 Statistical Test for Difference of Population Means

Our last (!) test applies to differences of means. Such tests are very common when you conduct a study involving two groups. In many medical trials, for example, subjects are randomly divided into two groups. One group receives a new drug, the second receives a placebo (sugar pill). Then the researcher measures any differences between the two groups.

Fortunately, we know how to do Hypothesis testing, and in this case we will exclusively use Excel to perform the caluclations for us. Here is the setup for this test:

• Null Hypothesis: two means M₁ and M₂ differ by a fixed amount c, i.e. M₁ - M₂ = c
• Alternative Hypothesis: the two means M₁ and M₂ do not differ by the amount c, i.e. M₁ - M₂ not equal to c (2-tail)
  
• Test Statistics: as computed by Excel
• Rejection Region: probability as computed by Excel

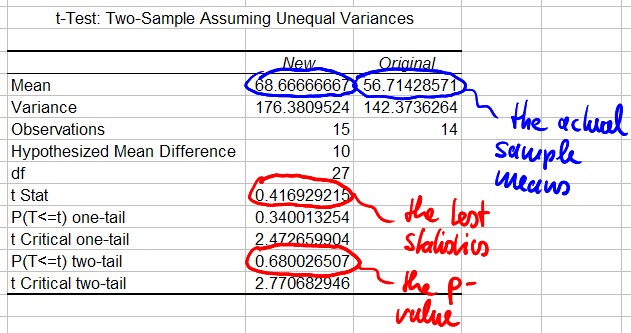
Example 1: Two procedures to determine the amylase in human body fluids were studied. The "original" method is considered to be an acceptable standard method, while the "new" method uses a smaller volume of water, making it more convenient as well as more economical. It is claimed that the amylase values obtained by the new method average at least 10 units greater than the orresponding values from the orignal method. A test using the original method was conducted on 14 subjects, the test with the new method on 15 subjects, giving the data displayed in the table below. Test the claim at the 1% level.

Original	New
38	46
48	57
58	73
53	60
75	86
58	67
59	65
46	58
69	85
59	74
81	96
44	55
56	71
50	63
	74

We need to be careful as to which variable is the first and which is the second one. In our example we want to test whether the average for the new method is 10 units larger than the old average. Since our procedure always tests M₁ - M₂ we have to pick as M₁ the "new method" data and as M₂ the "original method" data. With those choices for M₁ and  M₂   the statistical test corresponding to our example is setup as follows:

• Null Hypothesis:  M₁ - M₂ = 10
  
• Alternative Hypothesis: M₁ - M₂ not equal to 10
  

To continue, start Excel and enter the above data. Note that you do not really need to enter the first column, only the data for the original and new method is relevant.

Select Tools | Data Analysis ... then select t-Test: Two Sample, Assuming Unequal Variance

There are several two-sample tests available, for specific situations. A t-test assuming unequal variance is the most general one so select that. You should see a dialog window similar to the following:

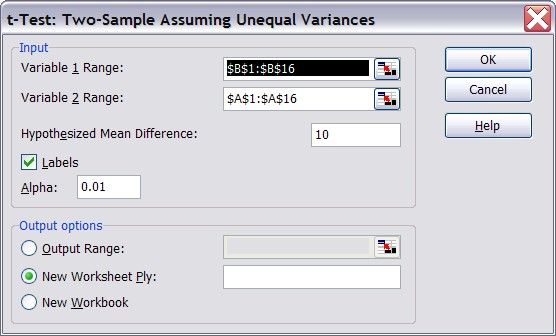
Since we picked the "new method" data as variable 1 we need to put the data for the second column in the "variable 1" range and the first column data in the "variable 2" range:

• In the Variable 1 Range: enter the range for the data from the "New" method (column B)
  
• In the Variable 2 Range: enter the range for the data from the "Original" method (column A)
  
• In the Hypothesized Mean Difference: enter the number 10
• For the Alpha value: enter the number 0.01
• Make sure to check the Labels box and click on Okay.

Excel will produce output similar to the following:

This output computes the mean and standard deviations of both variables, but most importantly computes the numbers needed to complete our test:

• Test Statistics: as computed by Excel, t = 0.4169
  
• Rejection Region: probability as computed by Excel: p = 0.68 (2-tail)
  

Thus, since the probability of the type-1 error is 0.68, or 68%, which is pretty large (definitely larger than 1%), our conclusion that the test is inconclusive. In other words, we found no significant evidence that the average of the new and old method differ by 10.

Comments:

• Excel requires that the hypothesized difference is not negative. If you want to test for a negative difference, switch the variables around and the difference will be positive.
  
• The actual difference, for this data, is 68.66 - 56.71 = 11.95. That difference is different from 10, but not significantly different, according to our test.

Example 2: Using the above data, is there enough evidence at the 0.05-level to conclude that there is a difference between the new and old method ?

To test whether there is a difference we simply set the hypothesized difference to 0 (in which case it actually does not matter which variable is the first and which the second). Therefore we repeat the above test, but this time we enter 0 as hypothesized difference instead of 10 and 0.05 as our Alpha level. Excel will produce the following values as output (make sure to check it yourself):

• Null Hypothesis:  M₁ - M₂ = 0
  
• Alternative Hypothesis: M₁ - M₂  not equal to 0
  
• Test Statistics: as computed by Excel, t = 2.55242
  
• Rejection Region: probability as computed by Excel: p = 0.016668 (2-tail)
  

In this case the computed probability is 0.017, or 1.7%, which is smaller than our value of A = 0.05. Therefore, we reject the null hypothesis which means that there is a significant difference between the two variables - it is just not as pronounced as we tested originally.

Example 3: The data file employeenumeric-split.xls contains the salaries for the Acme Widget Company, separated by sex. Use that data to test the hypothesis that women make at least $10,000 less on average than men.

First we determine which salary should be variable 1 and which variable 2:

1. if women are variable 1 and men are variable 2, then women making $10,000 less than men means M₁ - M₂ = -10000
2. if men are variable 1 and women are variable 2, then women making $10,000 less than men means M₁ - M₂ = 10000

Since Excel's t-Test only works for non-negative hypothesized difference we have to select option 2. With that convention Excel will produce the following output (make sure to double-check it):

• Null Hypothesis:  M₁ - M₂ = 10000
  
• Alternative Hypothesis: M₁ - M₂  not equal to 10000
  
• Test Statistics: as computed by Excel, t = 4.10335
  
• Rejection Region: probability as computed by Excel: p = 5.089E-05 (2-tail)

 Since 5.089E-05 means 0.00005089 , the computed probability definitely warrants our rejection of the null hypothesis. Thus, the difference in average salary between men and women at the Acme Widget Company is at least $10,000. Note that our test actually confirms  that the difference is not equal to $10,000, but looking at the actual values of the means as computed by Excel we can clearly conclude that the difference must be more than $10,000 (it is certainly not less).

That's all, folks -:)