Permeability
In this exercise you will focus on diffusion, passive movement, osmosis, and dialysis. The four are closely related, but not synonymous. They are vital processes in living organisms, and understanding them helps one understand many features of human body function, such as blood pressure, how kidneys cleanse blood, why drinking sea water can be dangerous, and how an enema works. To prepare for this, you should study the material on diffusion, passive movement, osmosis, and dialysis in your textbook and lecture notes.
Diffusion is the movement of molecules or ions from a region in which they are more concentrated to a region in which they are less concentrated. Note that membranes are not in the definition. Direction of movement is down the gradient (= with the gradient). Passive movement is diffusion of molecules or ions through a selectively permeable membrane. That is, the ions or molecules in question will move through a membrane from the region of their greater concentration to the region of their lower concentration (down the gradient). In a biological setting it will almost always be movement of molecules or ions in solution that are of interest. That may be diffusion of a type of molecule from place to place within a cell compartment (without passing through a membrane) or, more often, it will be movement of a type of molecule from one solution to another solution through a membrane. *Passive movement and diffusion are not synonyms.* For instance, a gas such as methane may diffuse through the air (a mixture of other gases) in a room without any involvement of a membrane.
Osmosis is the special case of passive movement in which it is the solvent molecules (water, in living systems) whose movement through a membrane is the point of interest. Biological membranes are freely permeable to water; therefore, water molecules will diffuse through a selectively permeable membrane from one solution into another if there is a difference in water concentration on opposite sides of the membrane. If a membrane separates two solutions of different solute concentration, and if the membrane is impermeable (= not permeable) to the solute, then water molecules will move down the water gradient from the region of greater water concentration to the region of lower water concentration. That direction is from the solution of lower solute concentration (the hypotonic solution) to the solution of greater solute concentration (the hypertonic solution). Note that if the membrane allows water passage but prevents solute passage, then it is incorrect to say that a "solution" moves through the membrane. Be sure you grasp the differences among the vocabulary items: solute, solvent, and solution.
Dialysis is the case of passive movement in which one type of solute is separated from another type of solute (both in the same solution) by a selectively permeable membrane that allows one type of solute to pass but not the other. For example, some chemical waste molecules in the bloodstream will pass through membranes in the kidney to become urinary wastes, while other (beneficial) molecules such as proteins remain in the bloodstream because they are too large to pass through the same membranes. A kidney dialysis machine performs a similar function though not nearly as well as it happens in a kidney.
Since the solutions found in living systems are usually complex (many types of solutes), it is better to begin study of permeability principles with a simple solution, one type of solute dissolved in water, for example. In living systems it's important to remember that water (solvent) molecules readily cross membranes, as a rule. So, the solute molecules dissolved in water are not the only molecules of a solution to be considered as you study permeability. Suppose that the concentration of solute Z is higher on one side of a membrane than on the other side, AND suppose that the size of the membrane pores will allow the small water molecules to pass through but not the solute molecules (Z). That sets up a water gradient across the membrane, and water molecules will move from the side with the greater water concentration (and lower solute concentration) to the side with the lower water concentration (and higher solute concentration). Water moves down the water gradient.
Part A. Observation of diffusion of solutes.
The first thing to do is to set up a diffusion exercise. Once started, you can check it from time to time while you proceed with Part B. From the lab instructor get a small petri dish containing a "solidified" agar solution. Agar is a polysaccharide; when a dilute aqueous solution of agar is heated to boiling and then allowed to cool, the solution gels (like gelatin prepared at home) into a semisolid form. The gel layer in the dish is 1% agar (the solute) and 99% water, but it's not fluid as any other typical dilute solution would be. To study diffusion of a solute through a liquid, it's necessary to prevent any stirring of the liquid during the observation period. Even temperature fluctuations in the room could cause uneven heating/cooling of liquid in a container; that would cause convection currents (mixing) within the liquid. Thus, this 1% aqueous solution of agar prevents currents within the solution but still will allow movement of molecules through it by diffusion.
You see that two "wells" have been cut into the agar; their facing edges are 1.5 cm apart. From an eyedropper bottle carefully put 4-5 drops of bromphenol blue dye into one well and (from the other eyedropper bottle) 4-5 drops of HCl solution into the other well. Handle both solutions carefully; wear gloves. Don't overfill either well; keep the acid and dye inside the wells, not on the agar surface. Put the lid on the dish and set the dish on a piece of white paper toweling (so the dye edge can be easily seen), to be observed periodically during the next hour or so, while you go ahead with the rest of the work. Make a note of the time you start this. The HCl solution is colorless, so you won't be able to "see" the H+ ions diffusing through the agar solution, but you can see the blue dye move through the agar.
What to watch for:
1. Check this every 5 to 10 minutes to determine how long it takes for you to be able to see that the dye is definitely moving (by diffusion) into the agar, that is, away from its well.
2. Once the dye is definitely seen to be diffusing into the agar, does it seem to continue moving away from the well at that same rate during the next hour or so?
3. Watch for a "flattening" of the advancing dye edge on the side facing the well with the HCl. Remember, the protons (H+) are diffusing from their well toward the dye well, even though you can't see them with the naked eye.
4. When you see this dye edge "flattening," use a dissecting microscope to observe that flattening edge. Bromphenol blue is a pH indicator dye; it changes color from blue (purplish) to yellow as the pH falls below 4. Under the microscope, is that bluish dye edge really "flat?"
5. You're looking at the zone where the protons from the acid well are colliding with the dye molecules. Since the protons cause a color change of the dye molecules, it's easy to see where that zone is. Is that zone equidistant from the two wells? The molecular weight of bromphenol blue is 670 daltons; a proton's mass is one dalton. What does your observation here tell you about the effect of molecular weight (size of molecule or ion) on rate of diffusion?
6. Based on what you've seen here, do you think diffusion is an effective way to move substances from place to place in multicellular organisms? For example, would diffusion serve for moving inhaled oxygen from your lungs to your brain? Why/why not?
When you've completed this observation, discard the petri dish in the solid trash container.
Part B. Osmosis and dialysis
You will set up a series of "dialysis bags" Some of them will illustrate osmosis and some will illustrate dialysis. You will generate and analyze some data of your own. Since the handling of the dialysis bags is awkward for one person, you will work with a lab partner. You are expected (as the lab exam will expect) to do the calculations and plotting of data yourself; be sure you understand the underlying principles and use of the vocabulary.
The membrane and its pores. Today you will use a membrane that allows water molecules to pass freely but not sucrose (table sugar). The membrane you will use is called "dialysis tubing". It is an artificial (man-made) membrane, not a unit membrane as found in living systems. However, since it is similar in some important ways, we can use it as a model membrane as long as we recognize its limitations. If you could see its surface highly magnified, you'd see tiny pores in this membrane. The size of the pores is big enough for water, but not sucrose, to pass. Keep in mind this point that the membrane has pores; that's important in understanding the dialysis part of this work at the end.
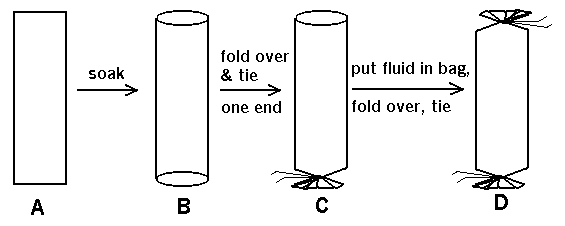
The dialysis tubing is supplied on a roll, like cellophane tape. When you
cut a segment of this and soak it in water to make it pliable, you see that
it's actually a flattened cylinder (see A, B in drawing below). If you fold
over and tie one end shut (water-tight) with thread (C in drawing below), you
can pour a solution into the tubing and tie the other end shut to make a
dialysis "bag" (D in drawing below).
If you put pure water in a dialysis bag and immerse it in pure water, the water
molecules will move randomly through the membrane in both directions. However,
there would be no net movement of water from one side to the other,
because there would be no water gradient. That is, the water
concentration is the same on both sides of the membrane. Suppose that instead
of water you put a solution in the bag, one that contained solute molecules of
a type too big to pass through the pores of the membrane. With pure water
outside the bag, water would diffuse from outside the bag into the solution in
the bag; that is, the water molecules would move down the water gradient
from where their concentration was greater (the pure water in this case) into
the solution that had a lower water concentration. Understand that this depends
on the assumption that the solute molecules on one side of the membrane cannot
pass through the membrane.
The net entry of water into the bag would cause it to swell. Suppose that you could apply just enough pressure to the bag surface to prevent this entry of water. That pressure that would have to be applied to the solution in the bag to prevent pure water (on the other side of the membrane) from diffusing into the bag is called the osmotic pressure of the solution in the bag. The osmotic pressure (O.P.) of pure water is zero; the O.P. value increases as you increase the solute concentration. A solution that has 10% salt in it has greater O.P. than a 5% salt solution.
NOTE WELL that osmotic pressure depends on the total number of solute molecules (or ions) dissolved per unit volume, not the types of solutes. This is an example of a colligative property. [Two other colligative properties that you may study in your chemistry coursework are elevation of boiling point and depression of freezing point.] Thus, a 0.1 M glucose solution, a 0.1 M sucrose solution, and a 0.1 M glycerol solution would have the same O.P. value since each contains the same number of solute molecules per unit of volume. However, molecules that dissociate or ionize in water, such as NaCl becoming Na+ and Cl- ions, contribute more than one osmotically active particle per molecule. A 0.1 M NaCl solution contains 0.1 mole of Na+ ions per liter of solution and 0.1 mole of Cl- ions per liter of solution. So 0.1 M NaCl solution would have twice the O.P. value that 0.1 M glucose solution has; glucose does not dissociate in solution. The terms, "osmole" and "osmolar" are used to recognize this distinction. An osmole is one mole of osmotically active particles. A one molar glucose solution, (1 M) is also 1 osmolar, since glucose does not dissociate in solution. But a one molar NaCl solution (1 M) is 2 osmolar, since NaCl does dissociate in solution. Similarly, a 1 M CaCl2 solution is 3 osmolar, since each CaCl2 dissociates into one Ca2+ ion and two Cl- ions. If you separate a 0.2 M sucrose solution from a 0.1 M sucrose solution by a membrane that is permeable only to water, then water would diffuse from the hypotonic (= hypoosmotic) 0.1 M sucrose solution into the hypertonic (= hyperosmotic) 0.2 M sucrose solution. Water molecules move down the water gradient across the membrane from the one solution into the other.
How to quantify osmosis. The net movement of water (by diffusion) into a dialysis bag could be measured simply by weighing the bag at various times. Water has mass, 1.0 g/mL. The weight gain of a bag reveals the amount of water that enters. What's more, the rate of osmosis is affected by the difference in water concentrations on opposite sides of the membrane. That is, if the water gradient across the membrane is more steep, then net movement of water will be faster. Of course, as the bag swells, the membrane itself begins to exert a pressure against the solution (as a balloon does when you blow more air into it). Then either the membrane bag would burst or the reverse pressure by the bag would ultimately slow down and even stop the net movement of water into the bag, even though the water concentration had not become equal on both sides of the membrane.
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
The basic setup. Using the procedure described below, and illustrated in the drawing above, you will prepare 6 dialysis bags containing water or various concentrations of sucrose solution or solutions of glucose or glycerol (instead of sucrose). You will immerse each bag in pure water in a plastic cup. You will use a balance (it's not a "scale") to measure the mass of each bag, to the nearest 0.1 g, at 0 minutes, 20 minutes, and 40 minutes. The 0 minutes weight (called "time zero") represents the weight of a bag before it is placed into the water in the cup. You will record these weight data in the Data Table (last page here), plot the corrected data, and interpret the data.
Potential sources of error and problems. In all lab work you must be alert to sources of error. Every source of error will affect your results and perhaps your interpretation of results. In fact, errors may be so numerous or so large in experimental work that the results are made worthless or that grossly incorrect conclusions are drawn. Therefore, one of the most important aspects of lab work, now and in the future, is to learn to recognize sources of error and to learn how to minimize them. You're expected to identify and evaluate sources of error in today's work. Here are some examples.
1. Both ends of each bag must be tied so as to be leak proof.
2. Handle the membranes carefully to avoid causing small punctures.
3. Keep the dialysis tubing moist and pliable as you work with it; it may crack
if it dries out.
4. Pour the solutions into the dialysis bags carefully to avoid spills and loss
of the solutions.
5. Note that as you prepare the bags, one by one, they will go into the water
in the cups at different clock times. So, your weighings of each bag at the 20
minute intervals must be staggered accordingly. Plan ahead so that you
will weigh each bag at the proper times.
6. Keep the balance pan clean and dry. Drops of liquid and dried sucrose on the
balance pan will add mass to your readings; that creates error.
7. When you remove the bags from the water in the cups to weigh them, be sure
you blot them well, especially at the tied ends, to remove water
adhering to the outer surface. Any liquid adhering to the outside of a bag will
add mass to your reading; that's error. You are interested in changes in weight
of the solutions inside the bags.
Materials needed.
- a 100 mL volumetric flask
- 7-inch segments of dialysis tubing (6)
- a spool of thread for tying dialysis bags
- a 25 mL graduated cylinder (1)
- 6 plastic cups (or beakers )
- a plastic funnel to help get the fluids into the
dialysis bags
- scissors for trimming thread
- grease pencil to label cups
- a bottle of water for preparing solutions
- a triple beam balance
- sucrose (in containers by the balances)
- weighing papers (by the balances)
- a wooden handle needle for piercing the bags when done
- 2 large test tubes for preparing sucrose dilutions
- a small bottle of 1 M glucose solution
- a small bottle of 1 M glycerol solution
- paper towels
- a 6-inch ruler for plotting data
Preparation
of the sucrose solutions.
1. Weigh 34.2 g of sucrose (molecular weight 342 daltons) on the balance; use a weighing paper and remember to correct for the paper's weight (tare weight). In this case the tare weight is small compared to the weight of the sucrose, but you must develop the habit of always correcting for the tare. Carefully pour the sucrose into the 100 mL volumetric flask; the funnel will help.
2. Gradually add water and swirl the flask until all of the
sucrose is dissolved. The final volume of the solution must be 100 mL;
the line on the neck of the flask marks 100 mL volume. Caution:
take care not to add a lot of water at the outset. You may overshoot the 100 mL
mark by the time all the sucrose is dissolved. Consider that the sugar
molecules occupy physical space, just as water molecules do. Therefore, if you measured 100 mL of water into
a beaker and dissolved 34.2 g of sucrose in that water, the volume of the
solution would be much more than the original 100 mL.
Several minutes are required to dissolve the sucrose. The final solution will
have a consistency that is almost like syrup.
This is a 1 M (1 molar) sucrose solution; it's also 34.2%,
weight-per-volume (w/v). That means that in each 1 mL volume of the solution
there is 0.342 g sucrose.
3. Label the 2 large test tubes #2 and #3. Use the graduated cylinder to measure 5 mL of this 1 M sucrose solution and 10 mL water into test tube #2. Then measure 10 mL of the 1 M sucrose solution and 5 mL water into test tube #3. Swirl each to mix uniformly. Calculate the concentrations of each of these new sucrose solutions. Leave these test tubes in the test tube rack for the moment. Rinse the graduated cylinder thoroughly.
Preparation of the membrane bags (dialysis bags).
1. Label the 6 cups #1 - #6. Fill each one with water almost to the top. Later as you place a dialysis bag in each cup, you need to have enough water in each cup to completely immerse each bag.
2. Into each cup put one of the flat pieces of dialysis tubing (the membrane); let them soak for about 5 minutes while you read ahead here to remind yourself of what you're about to do.
3. (After the soaking has made the dialysis membrane pieces pliable…) For each piece of tubing fold over one end about 3/8 inch and tie securely with doubled thread. See B & C in the previous drawing. This is awkward for a single pair of hands, so work with your partner to be sure that the folded end is tied securely. A leak later will jeopardize your results. Cut away the excess thread, but do not trim the dialysis tubing. Put each piece of tied tubing back into its cup to keep it wet until all 6 pieces are tied at one end; the tubing will crack and leak if it dries out.
4. With your partner, think through and organize the following work.
a. Once you've begun you must watch the time carefully so that you measure the weight of each bag at the proper time. You will use the graduated cylinder to dispense 15 mL of various fluids into the 6 bags; bags #2 and 3# will receive the 15 mL solutions that you've already prepared in the 2 test tubes.
b. Each of the 6 pieces of dialysis membrane is actually a flattened cylinder, tied now at one end. For each one, you will roll the untied end between your finger tips, to separate the sides of the tubing. When you see that bit of separation, insert the tip of the funnel carefully. You will then be able to slowly pour a solution through the funnel into the bag, minimizing error due to spill or overflow. The solutions that go into each bag are shown below.
c. Immediately after pouring the 15 mL into a bag, carefully fold over the open end and tie it shut with doubled thread, as shown in "D" in the previous drawing. Don't worry about the bit of trapped air in the bag.
d. Carefully blot dry the bag's surface, especially the tied ends where water may get trapped in the folded membrane, weigh the bag to the nearest 0.1 g, put the bag into its cup of water, and mark the time (time zero). Record this raw data value in the Data Table.
e. You will need to record the weight of each bag again at 20 minutes (then put it back into its cup) and at 40 minutes. To do that, dry each one's surface before weighing, and be sure to keep the balance pan clean and dry. NOTE THAT the bags go into their cups at different times since it will take about 3 minutes to prepare each bag. Therefore, the subsequent weighing times must be staggered also. You'll have to watch the clock carefully. Each raw data value is to be recorded in the Data Table.
5. The contents of the bags: Be sure to rinse the graduated cylinder well between uses.
Bag #1- 15 mL water
Bag #2- 5 mL of 1 M sucrose + 10 mL water (test tube #2 contents already prepared)
Bag #3- 10 mL of 1 M sucrose + 5 mL water (test tube #3 contents already prepared).
Bag #4- 15 mL of the 1 M sucrose solution (already prepared in the volumetric flask)
Bag #5- 15 mL of the 1 M glucose solution (in small bottle, as is)
Bag #6- 15 mL of the 1 M glycerol solution (in small bottle, as is)
Cleanup. After taking the 40 minute readings, and before you do the plotting and calculations:
a. Puncture and drain the dialysis bags over the sink, and discard the empty bags in the trash.
b. Thoroughly wash and rinse the volumetric flask, graduated cylinder, test tubes, and funnel to remove the solutions. They dry to leave a sticky mess if not cleaned properly. Invert the tubes and flask to drain in the rack. You will know when these things are cleaned adequately--- when you wouldn't mind drinking from them
c. Wash and rinse the cups and invert them to drain on paper towels.
d. Clean and dry the balance pan and clean the benchtop work area.
Calculations and plotting of data.
1. Correction of the raw data. Your recorded data in the Data Table right now are "raw" data; each value represents the weight of the membrane plus thread plus solution. But it is the weight of the solution and changes in that weight that are important. The weight of the bag and thread are the same and that factor doesn't change. Therefore, the weight of each solution is the total bag weight minus the weight of membrane plus thread. The membrane plus thread weight was predetermined as about 0.6 g. So, record the corrected values in the Data Table now. NOTE: we know that the water in bag #1 is not a solution, technically, but we group it with the others for convenience when referring to the set of six.
2. Percent data values. Having corrected the bag weights now, you'll notice that the weights of the six solutions were not the same at the start (time zero). Though each bag was supposed to receive 15 mL of a solution (or water in #1), two factors cause the initial bag weights to differ somewhat. First, your measurements and handling may cause slightly more or less than 15 mL to go into each bag (that's error). Second, the presence of the solutes affects the weights; for example, 1 mL of water weighs less that 1 mL of a sucrose solution. Then, if two solutions with different initial weights both gain 1 gram of weight due to water diffusing in, that 1 g of increase represents a larger change in one of the solutions than in the other. Therefore, to compare the weight changes in these solutions, we express the weight changes as percent of the starting weight. Round your percent vales to the nearest integer.
Example: If a 14.0 g solution (at time zero) weighs 15.1 g at 20 minutes and 16.0 g at 40 minutes, the percent data to be recorded in the Data Table are:
|
14.0
g X 100 =
100% |
15.1
g X 100 =
108% at 20 minutes |
16.
0 g X 100
= 114% at 40 minutes |
At time zero every solution is 100% of its own weight, and thereafter every solution's change in weight will be seen as relative to its starting weight. In this example the bag increased by 8% in 20 minutes and by a total of 14% in 40 minutes.
3. Data plot. Set up X-Y axes, with time on the X-axis and your "percent of time zero weight" on the Y-axis. Plot the 3 points (for 0, 20, 40 minutes) that you have for each solution. Connect the points for each solution; this is not a best fit straight line. Label the axes. Label each curve or use different symbols (with appropriate legend) to clearly show which curve represents which solution.
Interpretation (What does it mean?).
1. Effect of solute concentration on osmosis. Look at curves for #1- #4. These are a set; the solute is the same (sucrose) but the solute concentration is different. Since #1 has no sucrose, it is your "control" in the set. That's the sample against which all others are to be compared. Be able to explain the weight changes (% data) in these solutions: in terms of solute concentrations, in terms of water concentrations, in terms of gradients, in terms of hypertonic and hypotonic solutions. Why are the curves for the three sucrose solutions not the same? What does this tell you about the effect of steepness of a gradient on rate of diffusion through a membrane?
If you had continued to measure weights at 60 minutes, 80 minutes, and so on, would the solutions have increased in weight indefinitely? (Explain.) The answer to this question tells you why you're not supposed to draw a "best fit" straight line through the set of points. Do you see that? How long would it take, for any one of these solutions, to reach equilibrium? Explain.
Suppose you had placed bag #1 into a cup containing a sucrose solution. What would you expect to happen to its weight? Suppose you had placed bag #4 into a cup containing 1 M sucrose solution. What would you expect to happen to its weight?
The percent values for solution #1 should have been 100% at all three measurement times. Why? What might cause them to be slightly different at zero, 20, or 40 minutes?
2. Dialysis and evidence about membrane pore size. Look at curves #1, #4, #5, #6. These are a set; the concentration of solute is the same (1 M) but the type of solute is different: sucrose versus glucose versus glycerol. [You should already know structures of all three.] Again, #1 is your control; it contains no solute. These three solutes are structurally similar in having about one OH group per carbon atom. Molecular weights are 342 for sucrose (12 carbons), 180 for glucose (6 carbons), and 92 for glycerol (3 carbons). So, we can think of a glucose molecule as being about twice the size of a glycerol molecule and sucrose as being about twice the size of a glucose molecule.
You know, from lecture, that these three solutions should have the same osmotic pressure, since osmotic pressure is a colligative property. Therefore, the weight changes of these three solutions should be the same. Were they? But that assumes that the membrane here is impermeable to all three types of solutes. What happens if the pores in the membrane allow some types of solutes (smaller molecules) to pass through while restricting passage of others (larger molecules)? This guidesheet said earlier that the membrane pores allow water molecules (molecular weight = 18 daltons) to pass freely but prevent sucrose molecules from passing through. So what do your results tell you about the average size of the pores in this membrane?
Now suppose that you put into a membrane bag a solution containing sucrose and glycerol and placed that bag into a cup of water. Would both solutes remain inside the bag? If you had a simple chemical test for sucrose and another for glycerol, what would you find as you checked the liquid outside the bag at 20 minutes and 40 minutes? Then how would this be an example of dialysis?
Molarity calculation review
In the first lab session the guidesheet entitled "Introduction to Dilution Problems" showed you the relationship between different types of concentration expressions. In preparing the sucrose solutions in today's work you see again that concentration may be expressed as molarity or in the gram per liter (or g/mL) form or in the percent (w/v) form. Review that earlier guidesheet if necessary, to be sure that you're able to interconvert these concentration expression. For example, what is the molarity of a 50% (w/v) sucrose solution? If a glucose solution is 0.25 M, what is its concentration expressed as percent (w/v) or as mg/mL?
DATA TABLE (record weights to nearest 0.1 g; round % values to nearest
whole number)
|
|
||||
|
Bag
number |
Data
category |
0
minutes |
20
minutes |
40
minutes |
|
1 |
raw |
|
|
|
|
corrected |
|
|
|
|
|
percent |
|
|
|
|
|
2 |
raw |
|
|
|
|
corrected |
|
|
|
|
|
percent |
|
|
|
|
|
3 |
raw |
|
|
|
|
corrected |
|
|
|
|
|
percent |
|
|
|
|
|
4 |
raw |
|
|
|
|
corrected |
|
|
|
|
|
percent |
|
|
|
|
|
5 |
raw |
|
|
|
|
corrected |
|
|
|
|
|
percent |
|
|
|
|
|
6 |
raw |
|
|
|
|
corrected |
|
|
|
|
|
percent |
|
|
|
|