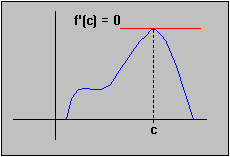
 Illustrating
Rolle'e theorem
Illustrating
Rolle'e theorem
If f is constantly equal to zero, there is nothing to prove. Hence,
assume f is not constantly equal to zero. Since f is a continuous
function on a compact set it assumes its maximum and minimum on
that set. One of them must be non-zero, otherwise the function
would be identically equal to zero. Assume for now that f(c) #
0 is a maximum. Since f(a) = f(b) = 0 we know that
c is in (a, b), and therefore f is
differentiable at c. Note that
f(x) 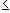 f(c)
since f(c) is a maximum.
f(c)
since f(c) is a maximum.
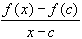
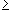 0 for all x <
c
0 for all x <
c
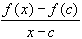
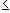 0 for all x >
c
0 for all x >
c
The first inequality implies that as x approaches c from the left, the limit must be greater than or equal to zero. The second one says that as x approaches c from the right, the limit must be less than or equal to zero. But since f is differentiable at c we know that both right and left handed limits exist and must agree. Therefore, f'(c) = 0.
The proof is similar if f(c) is a minimum. Can you see what would change, if anything ?
Note: As a consequence of this proof we have shown that if a differentiable function has a maximum or minimum in the interior of its domain then the derivative at that point must be zero.