Explain geometrically why (1+i)(1-i), i2, and (1+i)4 are all purely real numbers, i.e. the imaginary part of each answer will be zero.Context
Example 1.2.14 (a): Multiplying geometrically |
Explain geometrically why (1+i)(1-i), i2, and (1+i)4 are all purely real numbers, i.e. the imaginary part of each answer will be zero. |
Recall that Arg(z) is the principle angle of z. According to our result on multiplication of complex numbers that implies:
Arg(z*w) = Arg(z) + Arg(w)
If we apply that to our vectors we have:
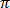/4 - 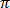/4 = 0
and a vector with angle 0 lies on the poitive real axis and is thus purely real.
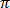/2 =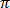
and a vector with angle 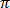lies on the negative
real axis and is thus purely real.
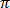/4 =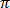
and a vector with angle 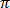lies on the negative
real axis and is thus purely real.