CS 1112 Exam 2 Sample Questions
![]()
Please answer, in your own words, the following questions:
CS 1112 Exam 2 Sample Questions
Please answer, in your own words, the following questions:
| What is Binary Search ? | |
| What is Recursion ? | |
| What is a Binary Search Tree ? |
![]()
Please look at the following code and circle any errors you see. Then disregard all lines containing errors and write down, for each "cout" statement, the value that would be printed.
SOME CODE GOES HERE
![]()
Please answer the following TRUE/FALSE questions:
| When using "binary search" to search an array, the array must be sorted. | |||||||
| When using "binary search" to search an array, the array must always be sorted in increasing order. | |||||||
When using "binary search" to search an array, and the arrays is not
sorted, then:
| |||||||
Suppose A is an array containing numbers in increasing order, but some numbers occur
more than once. When using a binary search for a value,
| |||||||
A binary tree of height 3
| |||||||
| The difference between a binary tree and a binary search tree is that a binary search tree has two children per node whereas a binary tree can have none, one, or two children per node. | |||||||
| A tree is an example of a list. | |||||||
| A list is an example of a tree. | |||||||
| A tree is a hierarchical data structure. | |||||||
| When you insert the values 40, 30, 60, 40, and 50 into a binary search tree, and then search for, say, 40, the search will find the second occurance of 40, not the first. | |||||||
Suppose you insert the values 40, 30, 60, 50, and 10 into a binary search tree, and then
use the following function:
void someOrder(Node *p)
{ if (p != 0)
{ someOrder(p->right);
cout << p->data << endl; someOrder(p->left);
}
}
then the output of calling someOrder(root) would be: 10, 30, 40, 50, , then 60. | |||||||
We discussed a "post-order" traversion function in class. As we have discussed
this class, it used
| |||||||
| A recursive function is a function that calls itself | |||||||
| If a recursive function does not have a base case it is likely to result in an infinite loop | |||||||
| If a recursive function does have a base case, it will never result in a recursive loop | |||||||
| A double-recursive function is a function that calls itself again, but doubles the input argument when calling itself. |
Click here for answers to true/false questions
![]()
Which of the following two trees is a binary search tree ?
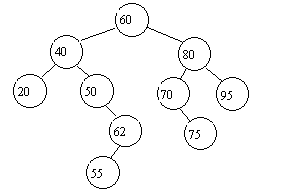 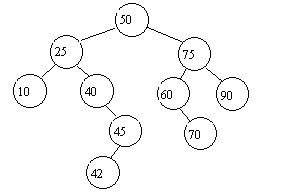 |
![]()
A tree could be represented either as a picture, or by listing the nodes in a specific order.
![]()
Consider the binary tree on the left. List each of the following:
|
|
![]()
Draw the binary search tree after each operation. Each insertion and deletion operates on
the original tree, and the new tree should again be a binary search tree. 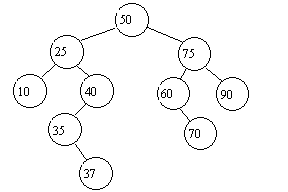
![]()
For a binary search tree, write C++ code that accomplishes the following:
b) A function that traverses the tree in inOrder and prints out the values of all nodes in the tree.
![]()
Explain, in your own words, how a binary search works on a sorted array [1..N] of
integers. Why is this search method preferred over a regular search ? What, if any are the
requirements to use this type of search
![]()
Write the code for a recursive binary search function on an array that is sorted in
decreasing order, i.e. starting with the largest value,
![]()
Consider the following functions defined recursively:
| What is the output for Mystery1(4), Mystery2(4), and Mystery3(4) ? | |
| The functions F1 and F2 can be described in much simpler terms. What, therefore, do these functions "really" do ? | |
| How often does the function Mystery1(4) call itself ? How often does the function Mystery(10) call itself ? How often does the function Mystery1(64) call itself, approximately ? |
![]()
| When using "binary search" to search an array, the array must be sorted. TRUE | |||||||
| When using "binary search" to search an array, the array must always be sorted in increasing order. FALSE | |||||||
When using "binary search" to search an array, and the arrays is not
sorted, then:
| |||||||
Suppose A is an array containing numbers in increasing order, but some numbers occur
more than once. When using a binary search for a value,
| |||||||
A binary tree of height 3
| |||||||
| The difference between a binary tree and a binary search tree is that a binary search tree has two children per node whereas a binary tree can have none, one, or two children per node. FALSE | |||||||
| A tree is an example of a list. FALSE | |||||||
| A list is an example of a tree. FALSE | |||||||
| A tree is a hierarchical data structure. TRUE | |||||||
| When you insert the values 40, 30, 60, 40, and 50 into a binary search tree, and then search for, say, 40, the search will find the second occurance of 40, not the first. FALSE | |||||||
Suppose you insert the values 40, 30, 60, 50, and 10 into a binary search tree, and then
use the following function:
void someOrder(Node *p)
{ if (p != 0)
{ someOrder(p->right);
cout << p->data << endl; someOrder(p->left);
}
}
then the output of calling someOrder(root) would be: 10, 30, 40, 50, then 60. FALSE | |||||||
We discussed a "post-order" traversion function in class. As we have discussed
this class, it used
| |||||||
| A recursive function is a function that calls itself TRUE | |||||||
| If a recursive function does not have a base case it is likely to result in an infinite loop TRUE | |||||||
| If a recursive function does have a base case, it will never result in a recursive loop FALSE | |||||||
| A double-recursive function is a function that calls itself again, but doubles the input
argument when calling itself. FALSE
|